Erlang入門

素晴らしい成果のために！

• ホーム
• FAQ
• RSS
• コード

再帰

再帰、こんにちは！

命令型プログラミング言語やオブジェクト指向プログラミング言語に慣れている読者の中には、ループがまだ紹介されていないことに疑問に思っている人がいるかもしれません。その答えは「ループとは何か？」です。実のところ、関数型プログラミング言語は通常、forやwhileのようなループ構造を提供しません。代わりに、関数型プログラマは再帰という面白い概念に頼ります。

序章で不変変数がどのように説明されたか覚えていると思います。覚えていない場合は、もう一度確認することができます！再帰は、数学的概念と関数を使って説明することもできます。値の階乗のような基本的な数学関数は、再帰的に表現できる関数の良い例です。数nの階乗は、数列1 x 2 x 3 x ... x nの積、またはn x (n-1) x (n-2) x ... x 1です。例を挙げると、3の階乗は3! = 3 x 2 x 1 = 6です。4の階乗は4! = 4 x 3 x 2 x 1 = 24です。このような関数は、数学表記では次のように表現できます。

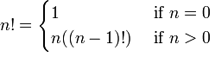
これは、nの値が0の場合は、結果1を返すことを意味します。0より大きい値の場合は、n-1の階乗とnを掛けた結果を返します。これは、1に達するまで展開されます。

4! = 4 x 3!
4! = 4 x 3 x 2!
4! = 4 x 3 x 2 x 1!
4! = 4 x 3 x 2 x 1 x 1

このような関数を数学表記からErlangに変換するにはどうすればよいでしょうか？変換は簡単です。表記の部分を見てみましょう：n!、1、n((n-1)!)、そしてif文。ここにあるのは、関数名（n!）、ガード（if文）、関数本体（1とn((n-1)!)）です。n!をfac(N)に名前変更して構文を少し制限すると、次のようになります。

-module(recursive).
-export([fac/1]).

fac(N) when N == 0 -> 1;
fac(N) when N > 0  -> N*fac(N-1).

これで階乗関数が完成しました！数学的な定義と非常によく似ています。パターンマッチングを使うと、定義を少し短くすることができます。

fac(0) -> 1;
fac(N) when N > 0 -> N*fac(N-1).

これは、本質的に再帰的な数学的な定義では簡単で迅速です。ループしました！再帰の定義は「自分自身を呼び出す関数」と簡単に述べることができます。ただし、無限ループを防ぐために停止条件（正式にはベースケース）が必要です。この場合、停止条件はnが0に等しいときです。その時点で、関数に自分自身を呼び出すよう指示することはなくなり、実行がそこで停止します。

長さ

少し実用的にしてみましょう。リストに含まれる要素の数を数える関数を実装します。そのため、最初に必要となるのは

• ベースケース。
• 自分自身を呼び出す関数。
• 関数を試すためのリスト。

ほとんどの再帰関数では、ベースケースを先に記述する方が簡単だと思います。長さを求めるために考えられる最も単純な入力は何でしょうか？空リストが最も単純で、長さは0です。そこで、長さに関して[] = 0であることを覚えておきましょう。次に単純なリストの長さは1です：[_] = 1。これで定義を始められると思います。次のように記述できます。

len([]) -> 0;
len([_]) -> 1.

素晴らしい！長さが0または1の場合は、リストの長さを計算できます！非常に便利です。もちろん役に立ちません。まだ再帰的ではないからです。これで、最も難しい部分、つまり1または0より長いリストに対して自分自身を呼び出すように関数を拡張する部分に進みます。先に述べたように、リストは[1 | [2| ... [n | []]]]として再帰的に定義されます。これは、[H|T]パターンを使用して1つ以上の要素のリストにマッチングできることを意味します。長さ1のリストは[X|[]]として定義され、長さ2のリストは[X|[Y|[]]]として定義されます。2番目の要素もリストであることに注意してください。つまり、最初の要素だけを数えればよく、関数は2番目の要素に対して自分自身を呼び出すことができます。リストの各値は長さ1としてカウントされるため、関数は次のように書き直すことができます。

len([]) -> 0;
len([_|T]) -> 1 + len(T).

これで、リストの長さを計算するための独自の再帰関数ができました。len/1が実行されたときの動作を確認するために、指定されたリスト、たとえば[1,2,3,4]で試してみましょう。

len([1,2,3,4]) = len([1 | [2,3,4])
               = 1 + len([2 | [3,4]])
               = 1 + 1 + len([3 | [4]])
               = 1 + 1 + 1 + len([4 | []])
               = 1 + 1 + 1 + 1 + len([])
               = 1 + 1 + 1 + 1 + 0
               = 1 + 1 + 1 + 1
               = 1 + 1 + 2
               = 1 + 3 
               = 4

これが正しい答えです。Erlangでの最初の役に立つ再帰関数の作成、おめでとうございます！

末尾再帰の長さ

4つの項のリストでは、関数の呼び出しを5つの加算の単一のチェーンに展開したことに気付いたかもしれません。これは短いリストでは問題ありませんが、リストに数百万の値がある場合は問題になる可能性があります。そのような単純な計算のために数百万個の数をメモリに保持したくありません。無駄であり、より良い方法があります。末尾再帰が登場します。

末尾再帰は、上記の線形プロセス（要素数だけ増える）を反復プロセス（実際には成長しない）に変換する方法です。関数の呼び出しを末尾再帰にするには、「単独」である必要があります。説明しましょう。以前の呼び出しを成長させたのは、最初の部分の答えが2番目の部分の評価に依存していたことです。1 + len(Rest)の答えを得るには、len(Rest)の答えを見つける必要があります。len(Rest)関数自体も、別の関数の呼び出しの結果を見つける必要がありました。加算は最後のものが見つかるまで積み重ねられ、その後に初めて最終結果が計算されます。末尾再帰は、発生時にそれらを削減することにより、この演算の積み重ねを排除することを目的としています。

これを実現するには、関数のパラメータとして追加のテンポラリ変数を持つ必要があります。階乗関数を用いてこの概念を説明しますが、今回は末尾再帰となるように定義します。前述のテンポラリ変数は、アキュムレータと呼ばれることもあり、呼び出しの増加を制限するために、計算結果を発生時に保存する場所として機能します。

tail_fac(N) -> tail_fac(N,1).

tail_fac(0,Acc) -> Acc;
tail_fac(N,Acc) when N > 0 -> tail_fac(N-1,N*Acc).

ここでは、tail_fac/1とtail_fac/2の両方を定義しています。その理由は、Erlangでは関数にデフォルト引数が許可されていないため（異なるアリティは異なる関数を意味します）、手動で行う必要があるためです。この特定のケースでは、tail_fac/1は末尾再帰のtail_fac/2関数の抽象化として機能します。tail_fac/2の非表示のアキュムレータに関する詳細は誰にも興味がないため、モジュールからtail_fac/1のみをエクスポートします。この関数を実行すると、次のように展開できます。

tail_fac(4)    = tail_fac(4,1)
tail_fac(4,1)  = tail_fac(4-1, 4*1)
tail_fac(3,4)  = tail_fac(3-1, 3*4)
tail_fac(2,12) = tail_fac(2-1, 2*12)
tail_fac(1,24) = tail_fac(1-1, 1*24)
tail_fac(0,24) = 24

違いがわかりますか？これで、メモリに2つ以上の項を保持する必要がなくなりました。空間使用量は一定です。4の階乗を計算するのに必要な空間と、100万の階乗を計算するのに必要な空間は同じです（4!の完全な表現が1M!よりも小さい数であることは無視してです）。

末尾再帰的な階乗の例を理解すれば、このパターンをlen/1関数にどのように適用できるかがわかるかもしれません。必要なのは、再帰呼び出しを「単独」にすることです。視覚的な例を好むなら、パラメータを追加することで、+1の部分を関数呼び出しの中に置くことを想像してください。

len([]) -> 0;
len([_|T]) -> 1 + len(T).

は

tail_len(L) -> tail_len(L,0).

tail_len([], Acc) -> Acc;
tail_len([_|T], Acc) -> tail_len(T,Acc+1).

になります。これで、長さ関数は末尾再帰になりました。

その他の再帰関数

さらにいくつかの再帰関数を記述して、もう少し慣れていきましょう。結局のところ、Erlangに存在する唯一のループ構造（リスト内包表記を除く）である再帰は、理解すべき最も重要な概念の1つです。後で試す他のすべての関数型プログラミング言語でも役立つため、メモを取ってください！

最初に記述する関数はduplicate/2です。この関数は、最初の引数として整数を、2番目の引数として他の項を取ります。その後、整数で指定された数の項のコピーのリストを作成します。これまでと同様に、まずベースケースを考えることが役立つでしょう。duplicate/2の場合、何かを0回繰り返すことが最も基本的なことです。項が何であっても、空リストを返すだけです。その他のすべてのケースでは、関数自体を呼び出すことでベースケースに到達しようとします。また、整数の負の値は禁止します。何かを-n回複製することはできないためです。

duplicate(0,_) ->
    [];
duplicate(N,Term) when N > 0 ->
    [Term|duplicate(N-1,Term)].

基本的な再帰関数ができたら、リストの構築をテンポラリ変数に移動することで、それを末尾再帰に変換することが容易になります。

tail_duplicate(N,Term) ->
    tail_duplicate(N,Term,[]).

tail_duplicate(0,_,List) ->
    List;
tail_duplicate(N,Term,List) when N > 0 ->
    tail_duplicate(N-1, Term, [Term|List]).

成功！ここで少し話題を変えて、末尾再帰とwhileループの類似点を示しましょう。tail_duplicate/2関数は、whileループの通常のすべての部分を持っています。Erlangのような構文を持つ架空の言語でwhileループを想像すると、関数は次のようになります。

function(N, Term) ->
    while N > 0 ->
        List = [Term|List],
        N = N-1
    end,
    List.

架空の言語とErlangの両方にあるすべての要素に注目してください。位置だけが変化します。これは、適切な末尾再帰関数は、whileループのような反復プロセスに似ていることを示しています。

また、リストの項を反転するreverse/1関数を記述することで、再帰関数と末尾再帰関数を比較したときに「発見」できる興味深い特性もあります。このような関数の場合、ベースケースは空リストであり、反転するものは何もありません。それが発生した場合は、空リストを返すだけです。その他の可能性はすべて、duplicate/2のように自分自身を呼び出すことでベースケースに収束しようとします。関数は、[H|T]パターンマッチングによってリストを反復処理し、Hをリストの残りの後に配置します。

reverse([]) -> [];
reverse([H|T]) -> reverse(T)++[H].

長いリストでは、これはまさに悪夢になります。すべての追加操作が積み重ねられるだけでなく、最後のものまでこれらの追加のそれぞれに対してリスト全体をトラバースする必要があります！視覚的な読者のために、多くのチェックは次のように表すことができます。

reverse([1,2,3,4]) = [4]++[3]++[2]++[1]
                      ↑    ↵
                   = [4,3]++[2]++[1]
                      ↑ ↑    ↵
                   = [4,3,2]++[1]
                      ↑ ↑ ↑    ↵
                   = [4,3,2,1]

ここで末尾再帰が救世主となります。アキュムレータを使用し、毎回新しいヘッダを追加するため、リストは自動的に反転されます。まず実装を見てみましょう。

tail_reverse(L) -> tail_reverse(L,[]).

tail_reverse([],Acc) -> Acc;
tail_reverse([H|T],Acc) -> tail_reverse(T, [H|Acc]).

これを通常のバージョンと同様の方法で表現すると、次のようになります。

tail_reverse([1,2,3,4]) = tail_reverse([2,3,4], [1])
                        = tail_reverse([3,4], [2,1])
                        = tail_reverse([4], [3,2,1])
                        = tail_reverse([], [4,3,2,1])
                        = [4,3,2,1]   

これは、リストを反転するためにアクセスする要素数が線形になっていることを示しています。スタックの増加を回避するだけでなく、はるかに効率的な方法で操作を実行します！

実装する別の関数はsublist/2です。これはリストLと整数Nを取り、リストの最初のN個の要素を返します。例として、sublist([1,2,3,4,5,6],3)は[1,2,3]を返します。繰り返しますが、ベースケースはリストから0個の要素を取得しようとすることです。ただし、sublist/2は少し異なります。渡されたリストが空の場合、2番目のベースケースがあります！空リストをチェックしないと、recursive:sublist([1],2).を呼び出したときにエラーがスローされますが、代わりに[1]が必要です。これが定義されると、関数の再帰的部分は、ベースケースのいずれかに達するまで、要素を保持しながらリストを循環するだけです。

sublist(_,0) -> [];
sublist([],_) -> [];
sublist([H|T],N) when N > 0 -> [H|sublist(T,N-1)].

これは、これまでと同じ方法で末尾再帰形式に変換できます。

tail_sublist(L, N) -> tail_sublist(L, N, []).

tail_sublist(_, 0, SubList) -> SubList;
tail_sublist([], _, SubList) -> SubList;
tail_sublist([H|T], N, SubList) when N > 0 ->
    tail_sublist(T, N-1, [H|SubList]).

この関数には欠陥があります。致命的欠陥です！リストをアキュムレータとして使用していますが、リストを反転させたときと全く同じ方法です。この関数をこのままコンパイルすると、sublist([1,2,3,4,5,6],3) は [1,2,3] ではなく [3,2,1] を返します。できることは、最終結果を受け取って自分で反転することだけです。tail_sublist/2 の呼び出しを変更し、再帰ロジックはそのまま残してください。

tail_sublist(L, N) -> reverse(tail_sublist(L, N, [])).

最終結果は正しく順序付けられます。テール再帰呼び出しの後でリストを反転させるのは時間の無駄のように思えるかもしれませんし、部分的には正しいでしょう（それでもメモリを節約できます）。短いリストでは、このため、通常の再帰呼び出しの方がテール再帰呼び出しよりもコードの実行速度が速くなる場合がありますが、データセットが大きくなると、リストの反転は比較的小さくなります。

さらに一歩進めて、ジップ関数を作成します。ジップ関数は、同じ長さの2つのリストをパラメータとして受け取り、2つの項をそれぞれ保持するタプルのリストとして結合します。独自のzip/2関数はこのように動作します。

1> recursive:zip([a,b,c],[1,2,3]).
[{a,1},{b,2},{c,3}]

パラメータの両方が同じ長さであることを考慮すると、基本ケースは2つの空のリストをジップすることになります。

zip([],[]) -> [];
zip([X|Xs],[Y|Ys]) -> [{X,Y}|zip(Xs,Ys)].

ただし、より寛容なzip関数が必要な場合は、2つのリストのいずれかが完了した時点で終了するように決定できます。このシナリオでは、したがって、2つの基本ケースがあります。

lenient_zip([],_) -> [];
lenient_zip(_,[]) -> [];
lenient_zip([X|Xs],[Y|Ys]) -> [{X,Y}|lenient_zip(Xs,Ys)].

基本ケースが何であっても、関数の再帰部分は同じままです。テール再帰関数を作成する方法を完全に理解するために、独自のテール再帰バージョンのzip/2とlenient_zip/2を作成することをお勧めします。それらは、メインループがそのように作成される大規模アプリケーションの中心的な概念の1つになります。

回答を確認したい場合は、recursive.erl、より正確にはtail_zip/2とtail_lenient_zip/3関数の私の実装をご覧ください。

クイックソート！

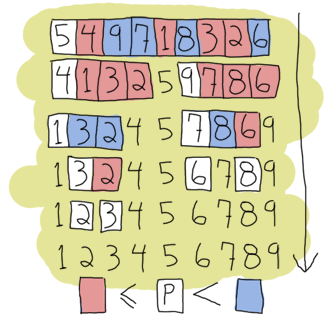
再帰とテール再帰が理解できると仮定できますが、念のため、より複雑な例であるクイックソートに進みます。はい、従来の「短い関数型コードを書けるよ」という標準的な例です。クイックソートの単純な実装は、リストの最初の要素（ピボット）を取り、ピボット以下の要素を新しいリストに入れ、それより大きい要素を別のリストに入れます。次に、これらの各リストに対して同じことを行い、各リストが小さくなるまで続けます。これは、ソートする空のリストしかなくなるまで続きます。これは基本ケースになります。この実装は、よりスマートなクイックソートのバージョンは、高速化のために最適なピボットを選択しようとするため、単純であると言われています。ただし、私たちの例では、それについては気にする必要はありません。

これには2つの関数が必要です。1つはリストをより小さな部分とより大きな部分に分割する関数、もう1つは新しい各リストに分割関数を適用してそれらを結合する関数です。まず、結合関数を記述します。

quicksort([]) -> [];
quicksort([Pivot|Rest]) ->
    {Smaller, Larger} = partition(Pivot,Rest,[],[]),
    quicksort(Smaller) ++ [Pivot] ++ quicksort(Larger).

これは、基本ケースを示しています。別の関数によって既に大小の部品に分割されているリスト、ピボットの両側のリストがクイックソートで追加されているピボットの使用です。これは、リストのアセンブルを担当するはずです。次に、パーティショニング関数です。

partition(_,[], Smaller, Larger) -> {Smaller, Larger};
partition(Pivot, [H|T], Smaller, Larger) ->
    if H =< Pivot -> partition(Pivot, T, [H|Smaller], Larger);
       H >  Pivot -> partition(Pivot, T, Smaller, [H|Larger])
    end. 

これで、クイックソート関数を実行できます。以前インターネットでErlangの例を探したことがある場合、別のクイックソートの実装、よりシンプルで読みやすい実装を見ているかもしれませんが、リスト内包表記を使用しています。簡単に置き換えられる部分は、新しいリストを作成する部分、partition/4関数です。

lc_quicksort([]) -> [];
lc_quicksort([Pivot|Rest]) ->
    lc_quicksort([Smaller || Smaller <- Rest, Smaller =< Pivot])
    ++ [Pivot] ++
    lc_quicksort([Larger || Larger <- Rest, Larger > Pivot]).

主な違いは、このバージョンの方がはるかに読みやすいことですが、その代わり、リストを2つの部分に分割するためにリストを2回トラバースする必要があります。これは明確性とパフォーマンスの戦いですが、本当の敗者は、lists:sort/1という関数が既に存在するため、あなたです。代わりにそれを使用してください。

リストだけではありません

この章を読むことで、Erlangの再帰は主にリストに関するものであると考え始めているかもしれません。リストは再帰的に定義できるデータ構造の良い例ですが、それ以外にも多くのものがあります。多様性の観点から、バイナリツリーの構築方法を見てから、そこからデータを読み取ります。

まず、ツリーとは何かを定義することが重要です。私たちの場合、それはずっと下までノードです。ノードは、キー、キーに関連付けられた値、さらに他の2つのノードを含むタプルです。これらの2つのノードのうち、1つはそれらを含むノードよりも小さく、もう1つはそれらを含むノードよりも大きいキーを持つ必要があります。だからこれが再帰です！ツリーは、ノードを含むノードで、それぞれがノードを含み、それらがさらにノードを含みます。これは永遠に続くことはできません（保存する無限のデータはありません）。そのため、ノードは空のノードを含むこともできると言います。

ノードを表すには、タプルが適切なデータ構造です。私たちの実装では、これらのタプルを{node, {Key, Value, Smaller, Larger}}（タグ付きタプル！）として定義できます。ここで、SmallerとLargerは、別の同様のノードまたは空のノード（{node, nil}）にすることができます。それ以上に複雑な概念は実際には必要ありません。

非常に基本的なツリーの実装のためのモジュールの構築を開始しましょう。最初の関数であるempty/0は、空のノードを返します。空のノードは新しいツリーの開始点であり、ルートとも呼ばれます。

-module(tree).
-export([empty/0, insert/3, lookup/2]).

empty() -> {node, 'nil'}.

その関数を使用して、ノードのすべての表現を同じ方法でカプセル化することで、ツリーの実装を隠すため、人々はそれがどのように構築されているかを知る必要がありません。その情報はすべて、モジュールだけで含めることができます。ノードの表現を変更することにした場合、外部コードを壊すことなく行うことができます。

ツリーにコンテンツを追加するには、まず再帰的にツリーをどのように移動するかを理解する必要があります。他のすべての再帰の例で行ったように、基本ケースを見つけることから始めましょう。空のツリーは空のノードであるため、基本ケースは論理的に空のノードです。空のノードに遭遇したときはいつでも、そこに新しいキー/値を追加できます。それ以外の場合は、コンテンツを配置する空のノードを見つけるためにツリーを通過する必要があります。

ルートから始めて空のノードを見つけるには、SmallerとLargerノードの存在により、挿入する新しいキーを現在のノードのキーと比較することで移動できるという事実を使用する必要があります。新しいキーが現在のノードのキーより小さい場合は、Smaller内の空のノードを見つけようとします。大きい場合は、Larger内を探します。ただし、まだ1つのケースがあります。新しいキーが現在のノードのキーと等しい場合はどうなりますか？そこには2つの選択肢があります。プログラムを失敗させるか、値を新しい値に置き換えるかのどちらかです。これがここで取るオプションです。このロジックをすべて関数に入力すると、次のようになります。

insert(Key, Val, {node, 'nil'}) ->
    {node, {Key, Val, {node, 'nil'}, {node, 'nil'}}};
insert(NewKey, NewVal, {node, {Key, Val, Smaller, Larger}}) when NewKey < Key ->
    {node, {Key, Val, insert(NewKey, NewVal, Smaller), Larger}};
insert(NewKey, NewVal, {node, {Key, Val, Smaller, Larger}}) when NewKey > Key ->
    {node, {Key, Val, Smaller, insert(NewKey, NewVal, Larger)}};
insert(Key, Val, {node, {Key, _, Smaller, Larger}}) ->
    {node, {Key, Val, Smaller, Larger}}.

ここで、関数は完全に新しいツリーを返すことに注意してください。これは、単一割り当てしかない関数型言語の典型です。これは非効率であると見なされる場合がありますが、ツリーの2つのバージョンの基盤となる構造の大部分は同じであることが多く、必要な場合にのみVMによってコピーされます。

このツリーの実装例で行う必要があるのは、キーを指定してツリーから値を見つけることができるlookup/2関数を作成することです。必要なロジックは、ツリーに新しいコンテンツを追加するために使用されるロジックと非常に似ています。ノードをステップ実行し、ルックアップキーが現在のノードのキーと等しいか、小さいか、大きいかを確認します。ノードが空の場合（キーがツリーにない場合）とキーが見つかった場合の2つの基本ケースがあります。プログラムがキーが見つからないたびにクラッシュするのを防ぐために、アトム'undefined'を返します。それ以外の場合は、{ok, Value}を返します。これは、ノードがアトム'undefined'を含んでいる場合、Valueだけを返すと、ツリーが正しい値を返したのか、見つからなかったのかを知る方法がないためです。成功したケースをこのようなタプルでラップすることで、どちらであるかを簡単に理解できます。実装された関数は次のとおりです。

lookup(_, {node, 'nil'}) ->
    undefined;
lookup(Key, {node, {Key, Val, _, _}}) ->
    {ok, Val};
lookup(Key, {node, {NodeKey, _, Smaller, _}}) when Key < NodeKey ->
    lookup(Key, Smaller);
lookup(Key, {node, {_, _, _, Larger}}) ->
    lookup(Key, Larger).

これで完了です。小さなメールアドレス帳を作成してテストしましょう。ファイルをコンパイルしてシェルを起動します。

1> T1 = tree:insert("Jim Woodland", "jim.woodland@gmail.com", tree:empty()).
{node,{"Jim Woodland","jim.woodland@gmail.com",
       {node,nil},
       {node,nil}}}
2> T2 = tree:insert("Mark Anderson", "i.am.a@hotmail.com", T1).
{node,{"Jim Woodland","jim.woodland@gmail.com",
       {node,nil},
       {node,{"Mark Anderson","i.am.a@hotmail.com",
              {node,nil},
              {node,nil}}}}}
3> Addresses = tree:insert("Anita Bath", "abath@someuni.edu", tree:insert("Kevin Robert", "myfairy@yahoo.com", tree:insert("Wilson Longbrow", "longwil@gmail.com", T2))).
{node,{"Jim Woodland","jim.woodland@gmail.com",
       {node,{"Anita Bath","abath@someuni.edu",
              {node,nil},
              {node,nil}}},
       {node,{"Mark Anderson","i.am.a@hotmail.com",
              {node,{"Kevin Robert","myfairy@yahoo.com",
                     {node,nil},
                     {node,nil}}},
              {node,{"Wilson Longbrow","longwil@gmail.com",
                     {node,nil},
                     {node,nil}}}}}}}

これで、それを使用してメールアドレスを検索できます。

4> tree:lookup("Anita Bath", Addresses).
{ok, "abath@someuni.edu"}
5> tree:lookup("Jacques Requin", Addresses).
undefined

リスト以外の再帰データ構造から構築された関数型アドレス帳の例はこれで終了です！Anita Bathさん、次は…

再帰的に考える

この章の内容を全て理解したのであれば、再帰的な思考がより直感的に理解できるようになっているはずです。再帰的な定義は、命令型（通常はwhileループやforループ）の対応物と比較して、段階的なアプローチ（「これをやって、それからあれをやって、それからこれをやって、完了」）ではなく、より宣言的なアプローチ（「この入力を受け取ったら、あれをやる、そうでなければこれをやる」）を取るのが特徴です。この性質は、関数ヘッダーのパターンマッチングを使うことでより明確になります。

それでも再帰の仕方が理解できない場合は、こちらを読むと役立つかもしれません。

冗談はさておき、パターンマッチングと組み合わせた再帰は、理解しやすい簡潔なアルゴリズムを作成するための最適な解決策となる場合があります。問題の各部分を、それ以上単純化できなくなるまで個別の関数に分割することで、アルゴリズムは、短いルーチンから得られる正しい答えを組み合わせるだけになります（これはクイックソートで行ったことと少し似ています）。この種のメンタルな抽象化は、通常のループでも可能ですが、再帰の方が実践しやすいと思います。結果は人それぞれです。

そして皆さん、議論です： *著者 vs. 著者自身*

• — はい、再帰は理解できたと思います。宣言的な側面も理解しました。不変変数のように数学的な根拠を持っていることも理解しました。場合によっては再帰の方が簡単であることも理解しました。他に何かありますか？
• — 規則的なパターンに従っています。基本ケースを見つけ、書き出します。それ以外のすべてのケースは、答えを得るためにこれらの基本ケースに収束しようとします。関数の記述が非常に簡単になります。
• — ええ、それは分かりました。何度も繰り返していましたね。私のループでも同じことができます。
• — そうですね。否定できません！
• — そうです。私が理解できないのは、末尾再帰の方が優れているのに、なぜこれほど多くの非末尾再帰バージョンを書いたのかということです。
• — ああ、それは単に理解しやすくするためです。より美しく理解しやすい通常の再帰から、理論的にはより効率的な末尾再帰に移行することは、すべての選択肢を示す良い方法のように思えました。
• — つまり、教育目的以外には役に立たないということですね、分かりました。
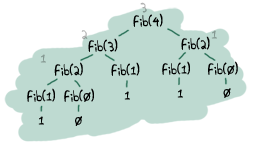
• — そうとは限りません。実際には、末尾再帰呼び出しと通常の再帰呼び出しのパフォーマンスの違いはほとんどありません。注意すべき点は、メインループのように無限ループするはずの関数です。また、常に非常に大きなスタックを生成し、遅く、末尾再帰にしなければ早期にクラッシュする可能性のある関数の種類もあります。フィボナッチ関数はその最たる例で、反復的または末尾再帰でない場合は指数関数的に増加します。 コードをプロファイリングして（やり方は後で説明します、約束します）、何が遅くなっているのかを見て、修正する必要があります。
• — しかし、ループは常に反復的で、これは問題になりません。
• — はい、でも…でも…私の美しいErlang…
• — まあ、素晴らしいですね！Erlangに'while'や'for'がないために、これだけの学習が必要だったんですね。ありがとうございました。Cでトースターのプログラミングに戻ります！
• — まだ待ってください！関数型言語には他にも利点があります！再帰関数の記述を容易にする基本ケースのパターンがいくつか見つかった場合、多くの賢い人々がさらに多くのパターンを見つけており、自分で再帰関数を記述する必要がほとんどなくなります。このまま続けていただければ、そのような抽象化をどのように構築できるかをお見せします。しかし、そのためには、より多くの力が必要です。高階関数について説明しましょう…

• < 前へ
• 目次
• 次へ >

特に明記されていない限り、このサイトのコンテンツはクリエイティブ・コモンズ 表示 - 非営利 - 変更禁止 ライセンスの下でライセンスされています。