素晴らしい Erlang を学ぼう

素晴らしい成果のために！

• ホーム
• FAQ
• RSS
• コード

関数型で問題を解決する

逆ポーランド記法電卓

ほとんどの人は、数値の間に演算子を置いた算術式を書くことを学びました（(2 + 2) / 5）。これは、ほとんどの電卓で数式を入力できる方法であり、おそらく学校で数えることを教わった表記法でしょう。この表記法には、演算子の優先順位について知っておく必要があるという欠点があります。乗算と除算は、加算と減算よりも重要です（より高い優先順位を持ちます）。

別の表記法があり、前置記法またはポーランド記法と呼ばれ、演算子は被演算子の前に来ます。この表記法では、(2 + 2) / 5 は (/ (+ 2 2) 5) になります。+ と / が常に 2 つの引数を取ると定義すると、(/ (+ 2 2) 5) は単に / + 2 2 5 と書くことができます。

ただし、ここでは逆ポーランド記法（または単にRPN）に焦点を当てます。これは前置記法の反対で、演算子は被演算子の後に続きます。上記の同じ例を RPN で記述すると、2 2 + 5 / となります。その他の例として、9 * 5 + 7 や 10 * 2 * (3 + 4) / 2 は、それぞれ 9 5 * 7 + および 10 2 * 3 4 + * 2 / に変換されます。この表記法は、初期の電卓モデルで非常に多く使用されていました。使用するメモリが少なくて済むからです。実際、RPN 電卓を持ち歩いている人もまだいます。これらの 1 つを作成します。

まず、RPN 式をどのように読むかを理解しておくとよいでしょう。1 つの方法は、演算子を 1 つずつ見つけてから、それらをアリティ（引数の数）によって被演算子と再グループ化することです。

10 4 3 + 2 * -
10 (4 3 +) 2 * -
10 ((4 3 +) 2 *) -
(10 ((4 3 +) 2 *) -)
(10 (7 2 *) -)
(10 14 -)
-4

しかし、コンピュータや電卓のコンテキストでは、より簡単な方法は、表示されるすべての被演算子のスタックを作成することです。数式 10 4 3 + 2 * - を例にとると、最初に見える被演算子は 10 です。これをスタックに追加します。次に 4 があるので、これもスタックの一番上にプッシュします。3 番目には 3 があります。これもスタックにプッシュしましょう。これで、スタックは次のようになります。

次に解析する文字は + です。これはアリティ 2 の関数です。これを使用するには、2 つの被演算子を供給する必要があります。これはスタックから取得されます。

そこで、その 7 を取得してスタックの一番上にプッシュし直します（うーん、これらの汚い数字をあちこちに浮遊させておきたくありません！）。スタックは現在 [7,10] であり、式の残りは 2 * - です。次に 2 を取得してスタックの一番上にプッシュできます。そして、動作するために 2 つの被演算子を必要とする * が表示されます。もう一度、スタックから取得します。

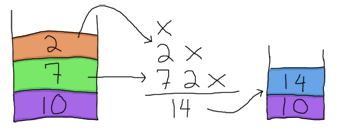
そして、14 をスタックの一番上にプッシュし直します。残りは - だけで、これも 2 つの被演算子が必要です。ああ、なんと素晴らしい！スタックには 2 つの被演算子が残っています。それらを使用しましょう！

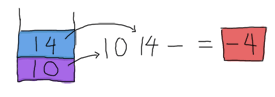
そして、結果が得られました。このスタックベースのアプローチは比較的間違いがなく、結果の計算を開始する前に実行する必要のある解析量が少ないため、古い電卓でこれを使用するのは良いアイデアでした。RPN を使用する他の理由もありますが、これはこのガイドの範囲外であるため、代わりにWikipedia の記事をご覧ください。

複雑なことを実行した後では、この解決策を Erlang で記述するのはそれほど難しくありません。難しいのは、最終結果を得るために必要な手順を理解することであることがわかりました。私たちはそれを実行したばかりです。素晴らしい。calc.erlという名前のファイルを開いてください。

最初に心配する必要があるのは、数式をどのように表現するかです。簡単に言うと、それらを文字列として入力するでしょう: "10 4 3 + 2 * -"。この文字列には空白がありますが、これは問題解決プロセスの一部ではありませんが、単純なトークナイザーを使用するために必要です。トークナイザーを通過した後、["10","4","3","+","2","*","-"] の形式の項のリストが使用可能になります。関数 string:tokens/2 がそれを行います。

1> string:tokens("10 4 3 + 2 * -", " ").
["10","4","3","+","2","*","-"]

それが私たちの式の適切な表現になります。次に定義する部分はスタックです。私たちはそれをどのように行うつもりですか？Erlang のリストがスタックのように機能していることに気付いたかもしれません。[Head|Tail] での cons (|) 演算子の使用は、Head をスタック (Tail、この場合) の一番上にプッシュするのと同じように効果的に動作します。スタックにリストを使用すれば十分でしょう。

式を読み取るには、手動で問題を解決したときと同じようにする必要があります。式から各値を読み取り、数値の場合はスタックに配置します。関数である場合は、スタックから必要なすべての値をポップし、結果をプッシュし直します。一般化するために、必要なのは、式全体をループとして一度だけ処理し、結果を累積することです。これは fold にとって完璧な仕事のように聞こえます！

計画する必要があるのは、lists:foldl/3 が式のすべての演算子と被演算子に適用する関数です。この関数は fold で実行されるため、2 つの引数を取る必要があります。最初の引数は処理する式の要素で、2 番目の引数はスタックになります。

calc.erl ファイルにコードの記述を開始できます。すべてのループを担当する関数と、式内の空白の削除も記述します。

-module(calc).
-export([rpn/1]).

rpn(L) when is_list(L) ->
    [Res] = lists:foldl(fun rpn/2, [], string:tokens(L, " ")),
    Res.

次に rpn/2 を実装します。式からの各演算子と被演算子はスタックの一番上に配置されるため、解決された式の結果はそのスタック上にあることに注意してください。ユーザーに返す前に、その最後の値をそこから取り出す必要があります。このため、[Res] でパターン マッチングを行い、Res のみを返します。

さて、より難しい部分です。rpn/2 関数は、渡されたすべての値に対してスタックを処理する必要があります。関数の先頭はおそらく rpn(Op,Stack) のようになり、その戻り値は [NewVal|Stack] のようになります。通常の数値を取得する場合、操作は次のようになります。

rpn(X, Stack) -> [read(X)|Stack].

ここで、read/1 は文字列を整数または浮動小数点値に変換する関数です。残念ながら、Erlang にはこれを行う組み込み関数はありません（どちらか一方のみ）。自分で追加します。

read(N) ->
    case string:to_float(N) of
        {error,no_float} -> list_to_integer(N);
        {F,_} -> F
    end.

ここで string:to_float/1 は "13.37" などの文字列を数値に変換します。ただし、浮動小数点値を読み取る方法がない場合、{error,no_float} が返されます。その場合は、代わりに list_to_integer/1 を呼び出す必要があります。

さて、rpn/2 に戻ります。遭遇するすべての数値がスタックに追加されます。ただし、パターンはすべてに一致するため（パターン マッチングを参照）、演算子もスタックにプッシュされます。これを回避するために、それらをすべて先行する句に配置します。最初に試すのは加算です。

rpn("+", [N1,N2|S]) -> [N2+N1|S];
rpn(X, Stack) -> [read(X)|Stack].

"+" 文字列に遭遇するたびに、スタックの上部から 2 つの数値（N1、N2）を取得し、それらを加算してから、結果をそのスタックにプッシュし直していることがわかります。これは、手動で問題を解決したときに適用したロジックとまったく同じです。プログラムを試してみると、動作することがわかります。

1> c(calc).
{ok,calc}
2> calc:rpn("3 5 +").
8
3> calc:rpn("7 3 + 5 +").
15

残りは簡単です。他のすべての演算子を追加するだけです。

rpn("+", [N1,N2|S]) -> [N2+N1|S];
rpn("-", [N1,N2|S]) -> [N2-N1|S];
rpn("*", [N1,N2|S]) -> [N2*N1|S];
rpn("/", [N1,N2|S]) -> [N2/N1|S];
rpn("^", [N1,N2|S]) -> [math:pow(N2,N1)|S];
rpn("ln", [N|S])    -> [math:log(N)|S];
rpn("log10", [N|S]) -> [math:log10(N)|S];
rpn(X, Stack) -> [read(X)|Stack].

対数のような引数を 1 つだけ取る関数は、スタックから 1 つの要素をポップするだけでよいことに注意してください。これまでに読み取ったすべての要素の合計またはすべての積を返す 'sum' や 'prod' などの関数を追加することは読者の練習問題として残します。手助けとして、それらはすでに私のバージョンのcalc.erlに実装されています。

これがすべて正常に動作することを確認するために、非常に単純なユニット テストを作成します。Erlang の = 演算子は、アサーション関数として機能できます。アサーションは予期しない値に遭遇するたびにクラッシュする必要があります。これはまさに私たちが必要としていることです。もちろん、Common Test や EUnit など、Erlang 用のより高度なテスト フレームワークがあります。後でそれらをチェックしますが、今のところ基本的な = で十分です。

rpn_test() ->
    5 = rpn("2 3 +"),
    87 = rpn("90 3 -"),
    -4 = rpn("10 4 3 + 2 * -"),
    -2.0 = rpn("10 4 3 + 2 * - 2 /"),
    ok = try
        rpn("90 34 12 33 55 66 + * - +")
    catch
        error:{badmatch,[_|_]} -> ok
    end,
    4037 = rpn("90 34 12 33 55 66 + * - + -"),
    8.0 =  rpn("2 3 ^"),
    true = math:sqrt(2) == rpn("2 0.5 ^"),
    true = math:log(2.7) == rpn("2.7 ln"),
    true = math:log10(2.7) == rpn("2.7 log10"),
    50 = rpn("10 10 10 20 sum"),
    10.0 = rpn("10 10 10 20 sum 5 /"),
    1000.0 = rpn("10 10 20 0.5 prod"),
    ok.

テスト関数はすべての操作を試みます。例外が発生しない場合、テストは成功したと見なされます。最初の 4 つのテストでは、基本的な算術関数が正しく動作することを確認します。5 番目のテストでは、まだ説明していない動作を指定します。try ... catch は、式が動作しないため、badmatch エラーがスローされることを期待しています。

90 34 12 33 55 66 + * - +
90 (34 (12 (33 (55 66 +) *) -) +)

rpn/1 の終了時に、スタックには -3947 と 90 の値が残ります。これは、そこに残っている 90 を処理する演算子がないためです。この問題を処理するには2つの方法があります。1つは無視してスタックの一番上の値（最後に計算された結果）だけを取得するか、算術が間違っているためクラッシュさせるかです。Erlang のポリシーではクラッシュさせることになっているため、ここではそれが選択されました。実際にクラッシュする部分は rpn/1 の [Res] です。これは、スタックに結果である要素が1つだけ残っていることを確認します。

true = FunctionCall1 == FunctionCall2 という形式のいくつかのテストがあるのは、= の左辺に関数呼び出しを持つことができないためです。比較の結果を true と比較することで、アサートのように動作します。

また、sum および prod 演算子のテストケースも追加したので、実装を練習できます。すべてのテストが成功すると、次のようになります。

1> c(calc).
{ok,calc}
2> calc:rpn_test().
ok
3> calc:rpn("1 2 ^ 2 2 ^ 3 2 ^ 4 2 ^ sum 2 -").
28.0

ここで、28 は実際に sum(1² + 2² + 3² + 4²) - 2 と等しくなります。必要に応じて、何度でも試してみてください。

電卓を改善するためにできることの1つは、不明な演算子やスタックに残された値が原因でクラッシュした場合に、現在の badmatch エラーではなく badarith エラーを発生させることです。これにより、calc モジュールのユーザーにとってデバッグが確実に簡単になるでしょう。

ヒースローからロンドンへ

次の問題も Learn You a Haskell からのものです。あなたは数時間後にヒースロー空港に着陸する飛行機に乗っています。できるだけ早くロンドンに着かなければなりません。あなたの裕福な叔父が死にかけており、あなたは彼の遺産を最初に主張したいのです。

ヒースローからロンドンへは2つの道路があり、それらを結ぶ小さな通りが多数あります。制限速度や通常の交通状況のため、道路や小さな通りによっては、他の場所よりも時間がかかる場合があります。着陸する前に、彼の家への最適な経路を見つけることで、チャンスを最大限に活かすことにします。これがあなたのラップトップで見つけた地図です。

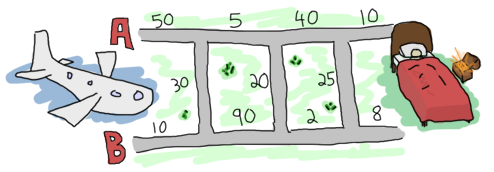
オンライン書籍を読んだ後、Erlang の大ファンになったあなたは、その言語を使用して問題を解決することにしました。地図を扱いやすくするために、road.txt という名前のファイルに次のようにデータを入力します。

50
10
30
5
90
20
40
2
25
10
8
0

道路は A1, B1, X1, A2, B2, X2, ..., An, Bn, Xn のパターンで配置されています。ここで、X は地図の A 側と B 側を結ぶ道路の1つです。最後の X セグメントとして 0 を挿入します。これは、どうやっても目的地にすでに到着しているためです。データは、{A,B,X} 形式の3つの要素（トリプル）のタプルで整理できる可能性があります。

次に、あなたが気づくのは、そもそも手で解決する方法を知らないのに、Erlang でこの問題を解決しようとしても無駄だということです。これを行うために、再帰が教えてくれたことを使用します。

再帰関数を記述する場合、最初に行うことは、ベースケースを見つけることです。目の前の問題の場合、これは分析するタプルが1つしかない場合、つまり、A、B （およびXを横断すること。この場合は、目的地にいるため無意味）の間で選択する必要がある場合です。

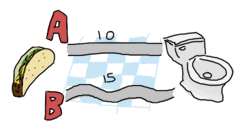
選択肢は、パス A とパス B のどちらが最短かを選ぶことだけです。再帰を正しく学習した場合は、ベースケースに収束しようとすべきであることを知っています。これは、各ステップで、次のステップで A と B のどちらかを選択する問題に問題を縮小したいということです。

地図を拡張して、最初からやり直しましょう。

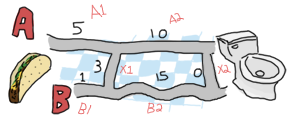
ああ！面白くなってきました！トリプル {5,1,3} を、A と B の厳密な選択にどのように縮小できるでしょうか？A に可能なオプションの数を見てみましょう。A1 と A2 の交差点（これを ポイント A1 と呼びます）に到達するには、道路 A1 を直接進む（5）か、B1 （1）から来て、X1 （3）を横断することができます。この場合、最初のオプション（5）は2番目のオプション（4）よりも長いです。オプション A の場合、最短パスは [B, X] です。では、B のオプションは何でしょうか？A1（5）から進んで X1（3）を横断するか、厳密にパス B1（1）を進むことができます。

わかりました！私たちが得たのは、最初の交差点 A へのパス [B, X] で長さ 4、および B1 と B2 の交差点へのパス [B] で長さ 1 です。次に、2番目のポイント A （A2 と終点または X2 の交差点）と2番目のポイント B （B2 と X2 の交差点）のどちらに行くかを決定する必要があります。決定を下すために、以前と同じようにすることをお勧めします。私がこのテキストを書いている人なので、あなたは従うしかありません。さあ行きましょう！

この場合に取り得るすべてのパスは、前のパスと同じ方法で見つけることができます。[B, X] からパス A2 を取ることで、次のポイント A に到達できます。これにより、長さ 14 (14 = 4 + 10) が得られます。または、[B] から B2 を取り、次に X2 を横断します。これにより、長さ 16 (16 = 1 + 15 + 0) が得られます。この場合、パス [B, X, A] は [B, B, X] よりも優れています。

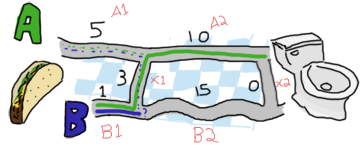
また、[B, X] からパス A2 を取り、次に長さ 14 (14 = 4 + 10 + 0) で X2 を横断するか、[B] から道路 B2 を取ることで、次のポイント B に到達できます。これにより、長さ 16 (16 = 1 + 15) が得られます。ここで、最適なパスは最初のオプション [B, X, A, X] を選択することです。

したがって、このプロセス全体が完了すると、長さ 14 の A または B の2つのパスが残ります。どちらも正しいものです。最後の X セグメントの長さが 0 であることを考えると、最後の選択では常に同じ長さの2つのパスがあります。問題を再帰的に解決することで、最後に常に最短のパスを得られるようにしました。悪くないでしょう？

微妙なことに、再帰関数を構築するために必要な基本的な論理部分が与えられました。必要に応じて実装できますが、自分たちで記述する再帰関数は非常に少なくすると約束しました。fold を使用します。

それで、私たちはどこにいたでしょうか？ああ、そうですね！入力としてフィードするファイルが準備できていました。ファイル操作を行うには、file モジュール が最適なツールです。ファイル自体を処理するために、多くのプログラミング言語に共通する多くの関数が含まれています（権限の設定、ファイルの移動、名前の変更と削除など）。

また、file:open/2 や file:close/1 （ファイルを開閉する！）、file:read/2 （ファイルの内容を文字列またはバイナリとして取得する）、file:read_line/1 （1行を読み取る）、file:position/3 （開いたファイルのポインタを指定された位置に移動するなど）、ファイルからの読み書きを行うための通常の関数も含まれています。

file:read_file/1 （バイナリとして内容を開いて読み取る）、file:consult/1 （Erlang の用語としてファイルを開いて解析する）や file:pread/2 （位置を変更してから読み取る）や pwrite/2 （位置を変更してコンテンツを書き込む）など、多数のショートカット関数も含まれています。

これらすべての選択肢が利用できるため、road.txt ファイルを読み込む関数を簡単に見つけることができます。道路が比較的小さいことを知っているため、file:read_file("road.txt").' を呼び出すつもりです。

1> {ok, Binary} = file:read_file("road.txt").
{ok,<<"50\r\n10\r\n30\r\n5\r\n90\r\n20\r\n40\r\n2\r\n25\r\n10\r\n8\r\n0\r\n">>}
2> S = string:tokens(binary_to_list(Binary), "\r\n\t ").
["50","10","30","5","90","20","40","2","25","10","8","0"]

この場合、スペース（" "）とタブ（"\t"）を有効なトークンに追加したので、ファイルは "50 10 30 5 90 20 40 2 25 10 8 0" の形式で書き込むこともできました。そのリストが与えられた場合、文字列を整数に変換する必要があります。RPN 電卓で使用したものと同様の方法を使用します。

3> [list_to_integer(X) || X <- S].
[50,10,30,5,90,20,40,2,25,10,8,0]

road.erl という新しいモジュールを開始して、このロジックを書きましょう。

-module(road).
-compile(export_all).

main() ->
    File = "road.txt",
    {ok, Bin} = file:read_file(File),
    parse_map(Bin).

parse_map(Bin) when is_binary(Bin) ->
    parse_map(binary_to_list(Bin));
parse_map(Str) when is_list(Str) ->
    [list_to_integer(X) || X <- string:tokens(Str,"\r\n\t ")].

関数 main/0 は、ファイルの内容を読み取り、parse_map/1 に渡す役割を担っています。関数 file:read_file/1 を使用して road.txt からコンテンツを取得するため、取得される結果はバイナリです。このため、関数 parse_map/1 をリストとバイナリの両方に一致するようにしました。バイナリの場合、文字列をリストに変換して、関数をもう一度呼び出すだけです（文字列を分割する関数はリストでのみ機能します）。

マップを解析する次のステップは、データを前に説明した {A,B,X} 形式に再編成することです。残念ながら、リストから一度に3つの要素をプルする簡単な汎用的な方法がないため、それを実行するには、再帰関数でパターンマッチングを行う必要があります。

group_vals([], Acc) ->
    lists:reverse(Acc);
group_vals([A,B,X|Rest], Acc) ->
    group_vals(Rest, [{A,B,X} | Acc]).

その関数は標準的な末尾再帰的な方法で動作します。ここでは、それほど複雑なことは何もありません。parse_map/1 を少し変更して呼び出すだけです。

parse_map(Bin) when is_binary(Bin) ->
    parse_map(binary_to_list(Bin));
parse_map(Str) when is_list(Str) ->
    Values = [list_to_integer(X) || X <- string:tokens(Str,"\r\n\t ")],
    group_vals(Values, []).

すべてをコンパイルしようとすると、意味のある道路が作成されるはずです。

1> c(road).
{ok,road}
2> road:main().
[{50,10,30},{5,90,20},{40,2,25},{10,8,0}]

ああ、はい、その通りですね。これで、畳み込み（fold）に適合する関数を記述するために必要なブロックが得られました。これが機能するためには、適切なアキュムレータを見つけることが必要です。

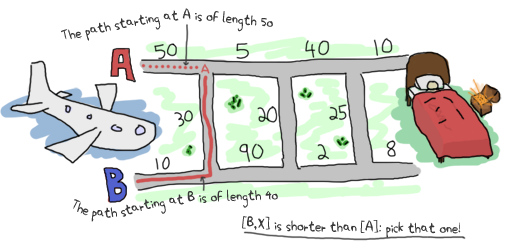
アキュムレータとして何を使用するかを決定するために、私が最も使いやすいと感じる方法は、アルゴリズムが実行されている最中の自分を想像することです。この特定の問題については、2番目のトリプル（{5,90,20}）の最短経路を見つけようとしているところを想像します。どの経路が最適かを決定するには、前のトリプルの結果が必要です。幸いなことに、私たちはそれを行う方法を知っています。アキュムレータは必要なく、すでにすべてのロジックを完了しているからです。したがって、Aの場合

そして、これら2つのパスの最短のものを取ります。Bの場合も同様でした。

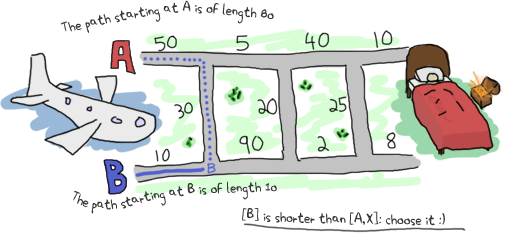
これで、Aから来る現在の最適なパスは[B, X]であることがわかりました。また、長さが40であることもわかっています。Bの場合、パスは単に[B]で、長さは10です。この情報を使用して、同じロジックを再適用することでAとBの次の最適なパスを見つけることができますが、前のものを式に含めて数えます。他に必要となるデータは、ユーザーに表示できるように、移動した経路です。2つのパス（A用とB用）と2つの累積長が必要なため、アキュムレータは{{距離A, パスA}, {距離B, パスB}}の形式を取ることができます。これにより、foldの各反復ですべての状態にアクセスでき、最後にユーザーに表示するために構築します。

これにより、関数に必要なすべてのパラメータが得られます。つまり、{A,B,X}トリプルと、{{距離A,パスA}, {距離B,パスB}}形式のアキュムレータです。

アキュムレータを取得するために、これをコードにすると、次のようになります。

shortest_step({A,B,X}, {{DistA,PathA}, {DistB,PathB}}) ->
    OptA1 = {DistA + A, [{a,A}|PathA]},
    OptA2 = {DistB + B + X, [{x,X}, {b,B}|PathB]},
    OptB1 = {DistB + B, [{b,B}|PathB]},
    OptB2 = {DistA + A + X, [{x,X}, {a,A}|PathA]},
    {erlang:min(OptA1, OptA2), erlang:min(OptB1, OptB2)}.

ここで、OptA1はAの最初のオプション（Aを経由）を取得し、OptA2は2番目のオプション（B、次にXを経由）を取得します。変数OptB1とOptB2は、ポイントBに対しても同様の処理を行います。最後に、取得したパスとともにアキュムレータを返します。

上記のコードで保存されたパスについて、各セグメントの長さをユーザーに知らせるのが良いかもしれないという単純な理由から、[x]ではなく[{x,X}]の形式を使用することにしたことに注意してください。私がもう一つ行っていることは、パスを逆方向に累積しているということです（{x,X}は{b,B}より前に来ます）。これは、私たちが末尾再帰であるfoldの中にいるためです。リスト全体が反転されるため、最後に走査したものを他のものの前に置く必要があります。

最後に、最短経路を見つけるためにerlang:min/2を使用します。タプルに対してそのような比較関数を使用するのは奇妙に聞こえるかもしれませんが、Erlangのすべての項は他のすべての項と比較できることを思い出してください。長さはタプルの最初の要素であるため、このようにソートできます。

残っているのは、その関数をfoldに組み込むことです。

optimal_path(Map) ->
    {A,B} = lists:foldl(fun shortest_step/2, {{0,[]}, {0,[]}}, Map),
    {_Dist,Path} = if hd(element(2,A)) =/= {x,0} -> A;
                      hd(element(2,B)) =/= {x,0} -> B
                   end,
    lists:reverse(Path).

foldの最後に、両方のパスは同じ距離になるはずですが、1つは最後の{x,0}セグメントを通過します。ifは両方のパスの最後に訪問した要素を見て、{x,0}を通過しないものを返します。ステップ数が最も少ないパスを選択する（length/1で比較する）こともできます。最短のものが選択されたら、反転されます（末尾再帰的に構築されました。必ず反転する必要があります）。その後、世界に表示するか、秘密にして裕福な叔父の遺産を手に入れることができます。そのためには、メイン関数を変更してoptimal_path/1を呼び出す必要があります。その後、コンパイルできます。

main() ->
    File = "road.txt",
    {ok, Bin} = file:read_file(File),
    optimal_path(parse_map(Bin)).

ほら、見てください！正しい答えが得られました！素晴らしい出来栄えです！

1> c(road).
{ok,road}
2> road:main().
[{b,10},{x,30},{a,5},{x,20},{b,2},{b,8}]

または、視覚的に表現すると

しかし、何が本当に役に立つでしょうか？Erlangシェル外からプログラムを実行できることです。メイン関数を再度変更する必要があります。

main([FileName]) ->
    {ok, Bin} = file:read_file(FileName),
    Map = parse_map(Bin),
    io:format("~p~n",[optimal_path(Map)]),
    erlang:halt().

メイン関数には、コマンドラインからパラメータを受け取るために必要な引数1のarityが与えられました。また、erlang:halt/0関数を追加しました。これは、呼び出された後にErlang VMをシャットダウンします。また、optimal_path/1の呼び出しをio:format/2でラップしました。これは、テキストをErlangシェル外に表示する唯一の方法だからです。

これらすべてにより、road.erlファイルは（コメントを除いて）次のようになります。

-module(road).
-compile(export_all).

main([FileName]) ->
    {ok, Bin} = file:read_file(FileName),
    Map = parse_map(Bin),
    io:format("~p~n",[optimal_path(Map)]),
    erlang:halt(0).

%% Transform a string into a readable map of triples
parse_map(Bin) when is_binary(Bin) ->
    parse_map(binary_to_list(Bin));
parse_map(Str) when is_list(Str) ->
    Values = [list_to_integer(X) || X <- string:tokens(Str,"\r\n\t ")],
    group_vals(Values, []).

group_vals([], Acc) ->
    lists:reverse(Acc);
group_vals([A,B,X|Rest], Acc) ->
    group_vals(Rest, [{A,B,X} | Acc]).

%% Picks the best of all paths, woo!
optimal_path(Map) ->
    {A,B} = lists:foldl(fun shortest_step/2, {{0,[]}, {0,[]}}, Map),
    {_Dist,Path} = if hd(element(2,A)) =/= {x,0} -> A;
                      hd(element(2,B)) =/= {x,0} -> B
                   end,
    lists:reverse(Path).

%% actual problem solving
%% change triples of the form {A,B,X}
%% where A,B,X are distances and a,b,x are possible paths
%% to the form {DistanceSum, PathList}.
shortest_step({A,B,X}, {{DistA,PathA}, {DistB,PathB}}) ->
    OptA1 = {DistA + A, [{a,A}|PathA]},
    OptA2 = {DistB + B + X, [{x,X}, {b,B}|PathB]},
    OptB1 = {DistB + B, [{b,B}|PathB]},
    OptB2 = {DistA + A + X, [{x,X}, {a,A}|PathA]},
    {erlang:min(OptA1, OptA2), erlang:min(OptB1, OptB2)}.

そして、コードを実行すると

$ erlc road.erl
$ erl -noshell -run road main road.txt
[{b,10},{x,30},{a,5},{x,20},{b,2},{b,8}]

そして、ええ、正しいです！物事を機能させるために必要なことはほぼすべてです。行を単一の実行可能ファイルにラップするためにbash/batchファイルを作成することも、同様の結果を得るためにescriptをチェックすることもできます。

これら2つの演習で見てきたように、問題を小さなパーツに分解して、すべてをまとめる前に個別に解決できる場合、問題を解決するのがはるかに簡単になります。また、理解せずに何かをプログラミングすることも価値がありません。最後に、いくつかのテストは常にありがたいものです。それらはすべてが正常に機能することを確認し、最終結果を変更せずにコードを変更できるようにします。

• < 前へ
• インデックス
• 次へ >

特に明記されていない限り、このサイトのコンテンツはクリエイティブ・コモンズ表示-非営利-改変禁止ライセンスの下でライセンスされています。